11. अंकीय उच्चता मॉडल
11. अंकीय उच्चता मॉडल
(The Digital Elevation Model)
अंकीय उच्चता मॉडल (DEM)
“किसी भी धरातल के उच्चावचों की भिन्नताओं की निरन्तरता का अंकीय प्रदर्शन अंकीय उच्चता मॉडल कहलाता है।” अर्थात यह उच्चावच को दर्शाने का एक कम्प्यूटर आधारित महत्वपूर्ण मॉडल है। पृथ्वी की सतह दिखाने के अलावा यह मॉडल ग्रहों एवं उपग्रहों के लिए भी प्रयोग किया जा रहा है। सामान्यतः धरातलीय विषमताओं को समोच्च रेखाओं द्वारा मानचित्र पर प्रदर्शित किया जाता है।
मूरे (Moore) तथा अन्य के अनुसार:-
अंकीय उच्चता मॉडल संख्याओं का क्रमिक विन्यास है जो समुद्र तल से ऊँचाई के धरातलीय वितरण को प्रदर्शित करता है।
अंकीय उच्चता मॉडल किसी दिये गये क्षेत्र के किसी बिन्दु की ऊँचाई का चित्रण अंकीय आकार में रखता है तथा सूचनाओं को किन्हीं कंकाल (Skeleton) रेखाओं के द्वारा एकत्र करता है। कंकाल रेखायें वे रेखायें होती हैं जो किसी ऊँचे-नीचे ढाल तथा ढाल परिवर्तन बिन्दुओं को दर्शाती है।
अंकीय भूभाग मॉडल (Digital Terrian Model)
उच्चावच को प्रदर्शित करने के लिए DTM शब्द का भी सामान्यतः उपयोग किया जाता है। अंकीय भूभाग मॉडल (DTM) धरातलीय लक्षणों के सतही वितरण को प्रदर्शित करता है।
अंकीय- भूभाग मॉडल (DTM), अंकीय आकार में भू-धरातलीय मानचित्र है जो केवल अंकीय उच्चता मॉडल को ही नहीं दर्शाता बल्कि भूमि उपयोग के प्रकारों, अधिवासों, सरिता रेखाओं के प्रकारों, ढालों इत्यादि को भी मॉडल के साथ दर्शाता है।
DEM शब्द उच्चता सम्बन्धी आँकड़ों को रखने के मॉडल के रूप में प्रयोग किया जाता है जबकि भूभाग (Terrain) शब्द अक्सर भूमि सतही ऊँचाई के अतिरिक्त स्थलरूपों के लक्षणों को भी प्रदर्शित करने के रूप में प्रयुक्त किया जाता है। यद्यपि DEM शब्द ही सबसे पहले उच्चता मॉडल के लिए प्रयोग किया गया था तब से लगातार द्विविम सतह के ऊपर Z लक्षणों के परिवर्तनों के लिए इसका प्रयोग किया जाता है।
अंकीय उच्चता मॉडल की आवश्यकता (Need of Digital Elevation Model)
अंकीय उच्चता मॉडल के कई उपयोग है। इनमें प्रमुख निम्न प्रकार से हैं:-
1. राष्ट्रीय आँकड़ा आधार प्रणाली में अंकीय भूपत्रक मानचित्रों के ऊँचाई सम्बन्धी आँकड़ों का संग्रह करने में यह महत्वपूर्ण भूमिका निभाता है।
2. यह सांख्यिकीय विश्लेषण तथा अलग-अलग भूभागों में तुलना करने में सहायक है।
3. DEM के द्वारा किसी भी क्षेत्र का ढाल मानचित्र, ढाल पहलू मानचित्र, भूआकृतिक विश्लेषण तथा अपरदन तथा बाह्य जल का अनुमान लगाया जा सकता हैं।
4. सामरिक उद्देश्यों के लिये भूआकृतियों का त्रिविम प्रदर्शन से किसी भूभाग का ज्ञान, हथियारों का संचालन तथा पाइलट परिशिक्षण जैसे कार्यों में DEM से सहायता मिलती है।
5. किसी भी भूभाग की डिजाइन तथा योजना तैयार करने के लिये DEM का उपयोग जाता है।
6.. इसके द्वारा विकट धरातल पर सड़क के डिजाइन में कटान तथा भरण (Cut and (Fill) जैसी समस्याओं का समाधान निकाला जा सकता है
7. कई इन्जिनिरिंग परियोजनाओं जैसे कि बाँध, नगर, पावर लाइन तथा तकनीकि कार्यों में DEM का उपयोग सहायक होता है।
8. इनके द्वारा किसी देश के सीमा पार की दृश्यता का भी विश्लेषण किया जा सकता है।
9. DEM के साथ कई विषयी मानचित्रों जैसे कि भूमि उपयोग, मिट्टी, शैल विन्यास, भूस्खलन इत्यादि को इसके ऊपर डालकर प्रदर्शित किया जा सकता है।
10. यह किसी भूआकृति तथा भूआकृतिक प्रक्रियाओं के निम्न अनुरूपता मॉडल के लिये आँकड़े उपलब्ध कराता है।
11. इसमें किसी भी प्रदर्शित स्तर के ऊँचाई परिवर्तित करने की सुविधा उपलब्ध होती है जिससे कई तथ्यों का अनुमान लगाया जा सकता है।
अंकीय उच्चता मॉडल के विभिन्न संरचनायें (Various Structure of DEM)
वर्तमान समय में DEM की कई प्रकार की संरचनायें प्रयोग की जाती हैं। इनमें से कोई भी पूर्ण रूप से किसी आँकड़ा संरचना की पूर्ति नहीं करते हैं। उद्देश्यों एवं कम्प्यूटर पर उपलब्धता के आधार पर निम्न उपयुक्त मॉडल प्रयोग किये जाते हैं-
1. रेखीय मॉडल (Linear Model)
2. असतत त्रिभुजीकृत जाल (Traingulated Irregular Network)
3. ग्रिड जाल (Grid Network)/वर्ग संरचना (Grid Structure)
1. रेखीय मॉडल (Linear Model):-
रेखीय मॉडल समोच्च रेखाओं के द्वारा किसी भू-भाग की ऊँचाई को प्रदर्शित करता है तथा प्रत्येक सम्मोच्च रेखा के X एवं Y निर्देशांकों के जोड़े ऊँचाई को व्यक्त करते हैं। सम्मोच्च रेखाओं से त्रिविम्ब प्रदर्शन तैयार किया जा सकता है तथा धरातलीय विशेषताओं को तब इसके ऊपर विश्लेषण किया जा सकता है।
इन रेखाओं के द्वारा निष्कोण (Smooth) दूरी के साथ सम्मोच्च रेखाओं की अनुपातिक दूरी को सम्मिलित जाता है जो किसी भी ढाल के निष्कोणता को दर्शाता है। सम्मोच्च रेखाओं के अनुरूप एक विशेष प्रकार का दूसरा रेखीय मॉडल भी है जो सरिताओं की व्याख्या करता है तथा जिसे जल प्रवाह मॉडल में भी प्रयोग किया जाता है। जैसा कि स्पष्ट है कि किसी भी रेखीय अंकीय ग्राफ को तैयार करने के लिये भूपत्रक मानचित्रों से सम्मोच्च रेखाओं को डिजिटाइज किया जाता है। ये मानचित्र ही आँकड़ों के ऐसे स्रोत हैं जो वर्गाकार खानों के द्वारा ऊँचाई मॉडल का निर्माण करते हैं।
2. असतत त्रिभुजीकृत जाल (Traingulated Irregular Network-TIN):-
असतत त्रिभुजीकृत जाल, अंकीय उच्चता मॉडल के लिये एक प्रणाली है जिसे पीउकेर तथा अन्य (1978) के द्वारा डिजाइन किया गया है। यह प्रणाली उच्चावच मैट्रिक्स के बहुलता (Redundancies) को दूर करता है। साधारण बोलचाल की भाषा में इसे टिन मॉडल कहते हैं।
टिन एक विक्टर स्थानविज्ञान संरचना के समान है। इसके अन्तर्गत पोलीगन जाल की स्थान विज्ञान संरचना के अनुरूप प्रदर्शित किया जाता है। टिन मॉडल आँकड़ा आधार के प्रारम्भिक प्रविष्टियों के जाल का नोड (Note) बनाने में सहायक होते हैं। आँकड़ा आधार में स्थान विज्ञान के सम्बन्ध एक-दूसरे से बनाये जाते हैं। प्रत्येक नोड को प्रत्येक निकट के नोड से किसी निशान के द्वारा निर्मित किया जाता है।
टिन मॉडल घरातल को त्रिभुजाकार समतल तत्वों में विभाजित करता है। भूभाग धरातल किसी जोड़ (नोड) द्वारा प्रतिदर्श होता है। ये धरातलीय बिन्दु भूभाग की विशेषताओं को स्थिति को दर्शाते हैं। त्रिभुजाकार आवृत्ति के तीन नोड सन्दर्भ बिन्दु होते है। इन बिन्दुओं को अन्तर्वेशन (Interpolation) विधि द्वारा बदला नहीं जा सकता है। धरातलीय प्रतिदर्श (Sampling) के अनतर्गत विशेष बिन्दुओं एवं रेखाओं को सम्मिलित किया जाता है जो कोई चोटी, गहरा भाग, ढाल रेखा जैसे कि जल विभाजक या सरिता रेखा तथा ढाल परिवर्तन रेखा को दर्शाया जाता है। ये कंकाल (Skeleton) रेखायें टिन संरचना पर किसी चाप की भाँति प्रतीत होती हैं। प्रतिचयन घनत्व भूभाग की जटिलता पर निर्भर करती है। नोड जाल के घनत्व की वृद्धि से धरातल की सही तस्वीर प्रस्तुत की जा सकती है परन्तु इसमें आँकड़ की अधिकता तथा परिकलन समय अधिक लगता है।
टिन संरचना के लाभ (Advantages of the Tin Structure)
1. टिन आँकड़ा संरचना एक संरचना है।
2. स्थानीय भूभाग की दशाओं के आवश्यकतानुसार त्रिभुजों की आकृति एवं आकार भिन्न-भिन्न होते हैं।
3. त्रिभुज के किनारों पर ढाल परिवर्तनशीलता की समाविष्टि करने में यह मॉडल सक्षम होता है।
4. टिन संरचना से कई भूभाग विशेषताओं जैसे कि ढाल, ढाल पहलू, इत्यादि का परिकलन किया जा सकता है।
टिन संरचना (TIN Structure ):-
सबसे महत्वपूर्ण कार्य संरचना की रूप-रेखा का है। प्रश्न यह है कि किस प्रकार सम्मोच्च रेखाओं के जाल को अंकों में परिवर्तित कर आँकड़ा आधार पर रखा जाता है। यहाँ पर आँकड़ा को आँकड़ा आधार पर रखने की विधियों को प्रदर्शित किया जा रहा है। टिन को आँकड़ों आधार (Data Base) में संग्रह करने के कई तरीके हैं। गुडचाइल्ड तथा केम्प (Goodchild and Kemp, 1990) ने दो संरचनाओं को प्रस्तावित किया है जो मुख्यतः त्रिभुजों तथा नोड़ों पर आधारित है । त्रिभुज संरचना ढाल विश्लेषण के लिये दण्ड विधि है जबकि नोड संरचना सम्मोच्च रेखाओं को निर्मित करने तथा आड़ा-तिरछा करने में सरल होती है।
त्रिभुजीकरण (Traingulation):-
टिन के निर्माण के लिये त्रिभुजाकार विधि का भी उपयोग जाता है। ग्राफ संरचना के साथ चापों एवं शीर्ष बिन्दुओं (Vertices) के उपयोग से क्षेत्र त्रिभुजों में उपविभाजित हो जाता है जिससे
(a) प्रत्येक मापन बिन्दु पर एक नोड निर्मित होता है तथा
(b) प्रत्येक त्रिभुज के अन्तर्गत तीन नोड होते हैं।
यह विधि आन्तरिक कोण को अधिकतम बनाती है तथा त्रिभुज की लम्बी भुजा को कम से कम करती है। इसी तरीके से भिन्नतायें प्राप्त की जाती है। इस विधि में सबसे पहले थिसेन (Thiessen) पोलीगॉन की रचना की जाती है। कृत्रिम त्रिभुजीकरण, अन्तरर्वेशन रेखाओं (Interpolation Lines) जैसे कि सम्मोच्य रेखायें त्रिभुज के किनारों पर एक दूसरे से आर-पार होती हैं। यह डेलाउनाइ (Delaunay) त्रिभुजीकरण पर आधारित है।
3. वर्ग संरचना (Grid Structure):-
वर्ग आधारित विधियाँ भी समान फैले त्रिभुजों या वर्गों के लिये प्रयोग हो सकते हैं। क्षेत्रीय तत्व तीन या चार पड़ोसी वर्ग बिन्दुओं से घिरा हुआ सेल (Cell) होता है। रास्टर आधारित जी.आई.एस. के अन्तर्गत वर्ग ग्रिड जाल का प्रयोग किया जाता है।
ग्रिड घनत्व या सेल का आकार क्षेत्रीय विषमताओं से आवश्यक रूप से समायोजित होता है। जहाँ पर भूभाग अत्यधिक कटाफटा है वहाँ पर ग्रिड घनत्व अधिक होता है। इस प्रकार के विषय क्षेत्रों में यह अतिरिक्त पुनरावृत्ति को बढ़ाता है। एक बात विशेषकर दिमाग में यह रखनी चाहिए कि जब सेल का सापेक्षिक आकार बड़ा होता है तो भूभाग तीव्र ढाल वाला होता है। इसके लिये अधिक आँकड़ों की आवश्यकता की पूर्ति होती है।
इस विधि का लाभ यह हैं कि इसमें आँकड़ों का संग्रह अतिसरल होता है। दूसरा इसके द्वारा DEM से कई परिकलन का निर्माण किया जा सकता है।
निष्कर्ष:
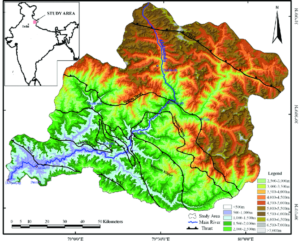
उपरोक्त तीनों विधियों में सबसे सरल एवं प्रचलित टिन संरचना प्रमुख है। टिन संरचना पर आधारित यहाँ पर हिमालय भूभाग (अलकनंदा क्षेत्र) का एक उच्चता मॉडल तैयार किया गया है। इसमें धरातलीय विषमताओं को उजागर किया गया है। इस प्रकार के धरातलीय मॉडल किसी भूभाग के मॉडलिंग करने में सहायक होते हैं।
प्रश्न प्रारूप
Q. अंकीय उच्चता मॉडल पर प्रकाश डालें।
(Throw light on the digital elevation model.)
Read More:
- 1. सुदूर संवेदन और भौगोलिक सूचना तंत्र
- 2. उपग्रहों के विकास के इतिहास / The Historical Development of Satellite
- 3. भूगोल में सुदूर संवेदन के महत्व एवं उपयोगिता / The Significance and Utility of Remote Sensing in Geography
- 4. सुदूर संवेदन प्लेटफार्म
- 5. भू-स्थैतिक उपग्रह, सूर्य तुल्यकालिक उपग्रह एवं ध्रुव कक्षीय उपग्रह
- 6. लैण्डसेट उपग्रह
- 7. भारतीय सुदूर संवेदन उपग्रह
- 8. The Aerial Photography (वायु फोटोग्राफी)
- 9. The Digital Image (डिजिटल इमेज)
- 10. Projection / प्रक्षेप
- 11. अंकीय उच्चता मॉडल
- 12. जी. आई. एस. की संकल्पनाओं एवं उपागम
- 13. भौगोलिक सूचना प्रणाली के उद्देश्यों, स्वरूपों एवं तत्वों की विवेचना
- 14. भू-सन्दर्भ / The Geo-Referencing System
- 15. डिजिटल मानचित्रकला
- 16. रास्टर एवं विक्टर मॉडल में अंतर
- 17. The application of G.P.S. (जी.पी.एस. के उपयोग)
- 18. सुदूर संवेदन के उपयोग
- 19. Classification of Aerial Photograps (वायु फोटोचित्रों का वर्गीकरण)
